C++で大きな数の掛け算の筆算をする

大学院の授業で、とても大きな数の掛け算を電卓で行うときの方法を考えよという問題があったので、その方法をC++で実装しました。ぶっちゃけそこまで大きい数を計算するならPython使えばよくね？って思いました。

1.筆算のやり方

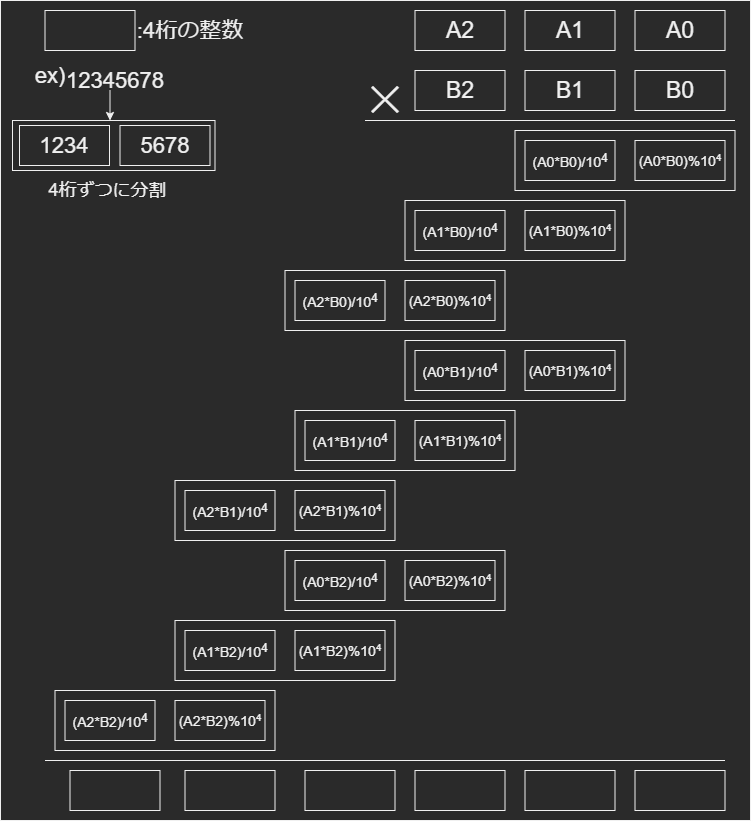
数字を任意の桁数で切り分けます。今回は4桁で切り分けています。

また、ブロックごとの演算の結果も4桁ごとに区切ります。上位4桁は10^4で割ったときの商で、下位4桁は10^4で割ったときの余りとして捉えると楽です。

それ以外は小学校で習った掛け算の筆算とやり方は同じです。

扱った問題では2数が定数なので、コード内でも定数にしています。

	#include <bits/stdc++.h>
	#define rep(i, n) for (int i = 0; i < (n); i++)
	#define rep2(i, s, n) for (int i = (s); i < (n); i++)
	using namespace std;
	using ll = long long;
	using P = pair<int, int>;
	int main() {
	//入力など
	string a = "98765432102468013579", b = "76309741852581470369";
	vector<int> ans(a.size() / 4 + b.size() / 4, 0);
	vector<int> x(a.size() / 4), y(b.size() / 4);

	//文字列を4文字ずつに分割し、int型に変換し配列に格納する
	rep(i, a.size() / 4) {
	x[i] = stoi(a.substr(i * 4, 4));
	y[i] = stoi(b.substr(i * 4, 4));
	}
	//筆算実装時の書きやすさのために要素を反転
	reverse(x.begin(), x.end());
	reverse(y.begin(), y.end());

	//筆算部分
	rep(i, a.size() / 4) {
	rep(j, b.size() / 4) {
	//ただの掛け算
	ans[i + j] += x[j] * y[i];
	//繰り上がり処理
	ans[i + j + 1] += ans[i + j] / 10000;
	ans[i + j] = ans[i + j] % 10000;
	}
	}
	//配列の並びと実際の筆算でのブロックの並びは逆なので反転
	reverse(ans.begin(), ans.end());

	//配列内の数値をstring型に変換。この時0埋めをする。
	string answer;
	for (int t : ans) {
	//数値をstring型に変換
	string tmp = to_string(t);
	// 0埋め部分
	ostringstream ss;
	ss << setw(4) << setfill('0') << tmp;
	string s(ss.str());
	//答えに結合
	answer += s;
	}
	string wrong_answer = "7536774627697996910549787129974478141651";
	int count = 0;
	rep(i, answer.size()) {
	if (answer[i] != wrong_answer[i]) count++;
	}
	cout << "Correct answer is " << answer << endl;
	cout << "Miss count is " << count << endl;
	return 0;
	}

by GitHub

配列の長さなどはstringの長さで決まるようにしているので、定数を変数に変えても動くはずです。

Pythonなら(実質)桁数無限だから、計算したいだけならばPythonを使おう。

はじめての離散数学 – 小倉久和 – 近代科学社(2011)